Boxplots

SDS 192: Introduction to Data Science

Lindsay Poirier
Statistical & Data Sciences, Smith College

Fall 2022

For Today

• Measures of Central Tendency and Dispersion
• Boxplots
• Project 1 Assigned

A measure of central tendency is a single numeric quantity describing data by identifying a central position.

Let’s create the following data frame to motivate today’s lecture.

library(tidyverse)
counties <- read_csv("https://raw.githubusercontent.com/sds-192-intro-fall22/sds-192-public-website-quarto/a8b64e3070ca2543b904d4d92780b09e6062ced6/website/data/nbi_counties.csv")
route_prefixes <- read_csv("https://raw.githubusercontent.com/sds-192-intro-fall22/sds-192-public-website-quarto/a8b64e3070ca2543b904d4d92780b09e6062ced6/website/data/nbi_route_pre.csv")
maintenance <- read_csv("https://raw.githubusercontent.com/sds-192-intro-fall22/sds-192-public-website-quarto/a8b64e3070ca2543b904d4d92780b09e6062ced6/website/data/nbi_maintenance.csv")
kinds <- read_csv("https://raw.githubusercontent.com/sds-192-intro-fall22/sds-192-public-website-quarto/a8b64e3070ca2543b904d4d92780b09e6062ced6/website/data/nbi_kind.csv")

nbi_ma <- read.delim("https://www.fhwa.dot.gov/bridge/nbi/2022/delimited/MA22.txt", sep = ",") |>
  left_join(counties) |>
  left_join(route_prefixes) |>
  left_join(maintenance) |>
  left_join(kinds) |>
  filter(SERVICE_ON_042A == 1) |>
  select(STRUCTURE_NUMBER_008, COUNTY_CODE_003_L, ROUTE_PREFIX_005B_L, MAINTENANCE_021_L, YEAR_BUILT_027, ADT_029, STRUCTURE_KIND_043A_L, STRUCTURAL_EVAL_067, BRIDGE_IMP_COST_094) |>
  mutate(STRUCTURE_KIND_043A_L = 
           case_when(
             STRUCTURE_KIND_043A_L == "Concrete continuous" ~ "Concrete",
             STRUCTURE_KIND_043A_L == "Steel continuous" ~ "Steel",
             STRUCTURE_KIND_043A_L == "Prestressed concrete continuous" ~ "Prestressed concrete",
             TRUE ~ STRUCTURE_KIND_043A_L)) |>
  mutate(BRIDGE_IMP_COST_094 = BRIDGE_IMP_COST_094 * 1000)

nbi_hampshire <- nbi_ma |> filter(COUNTY_CODE_003_L == "Hampshire")

rm(counties, kinds, maintenance, route_prefixes)

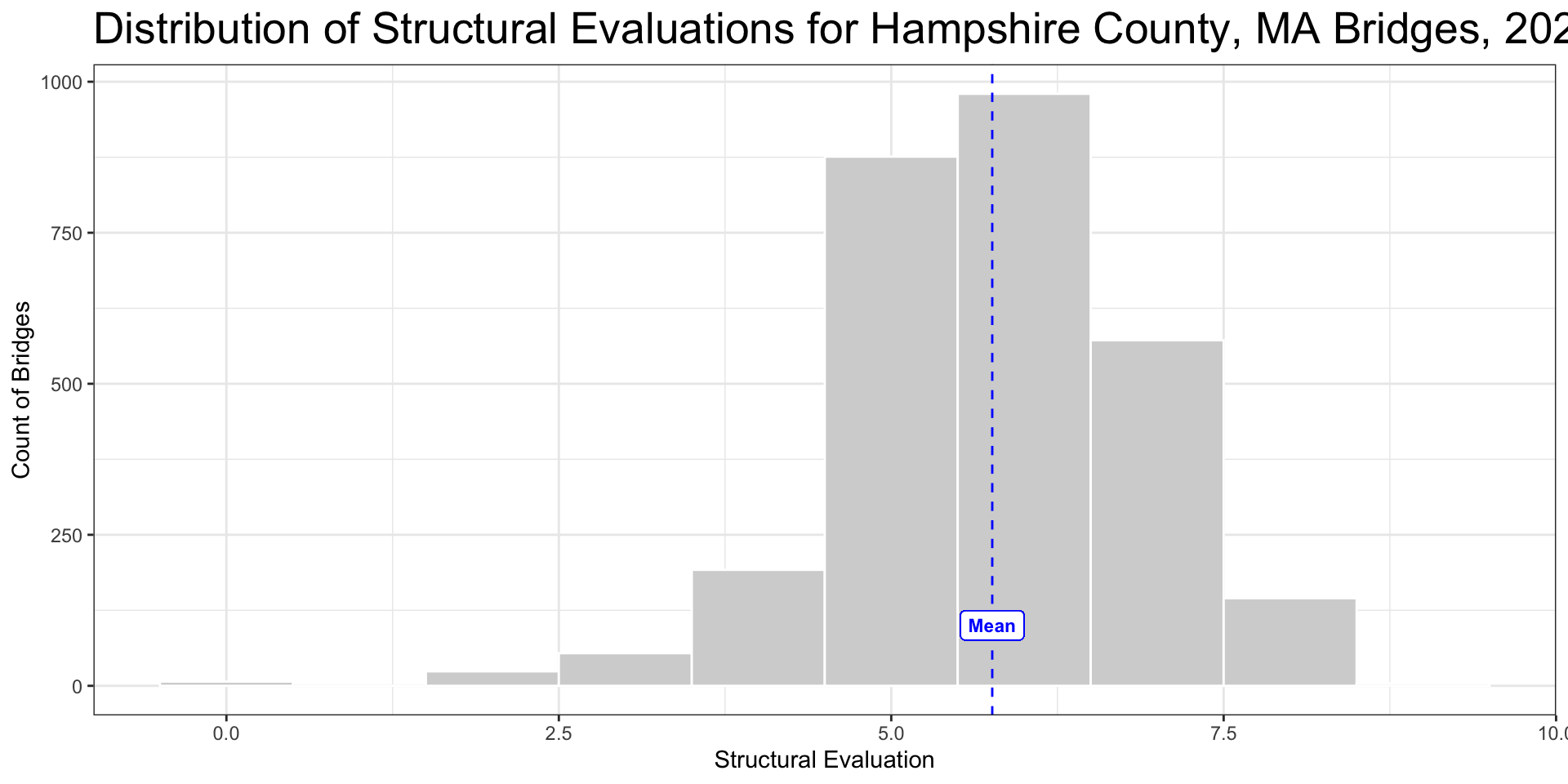
Mean

• Sum of values divided by number of values summed
• Takes every value into consideration
• Model of entire dataset
• Heavily influenced by outliers

Median

• Middle value(s) of the dataset when all values are lined from smallest to largest
• Does not model entire dataset
• Limited influence from outliers

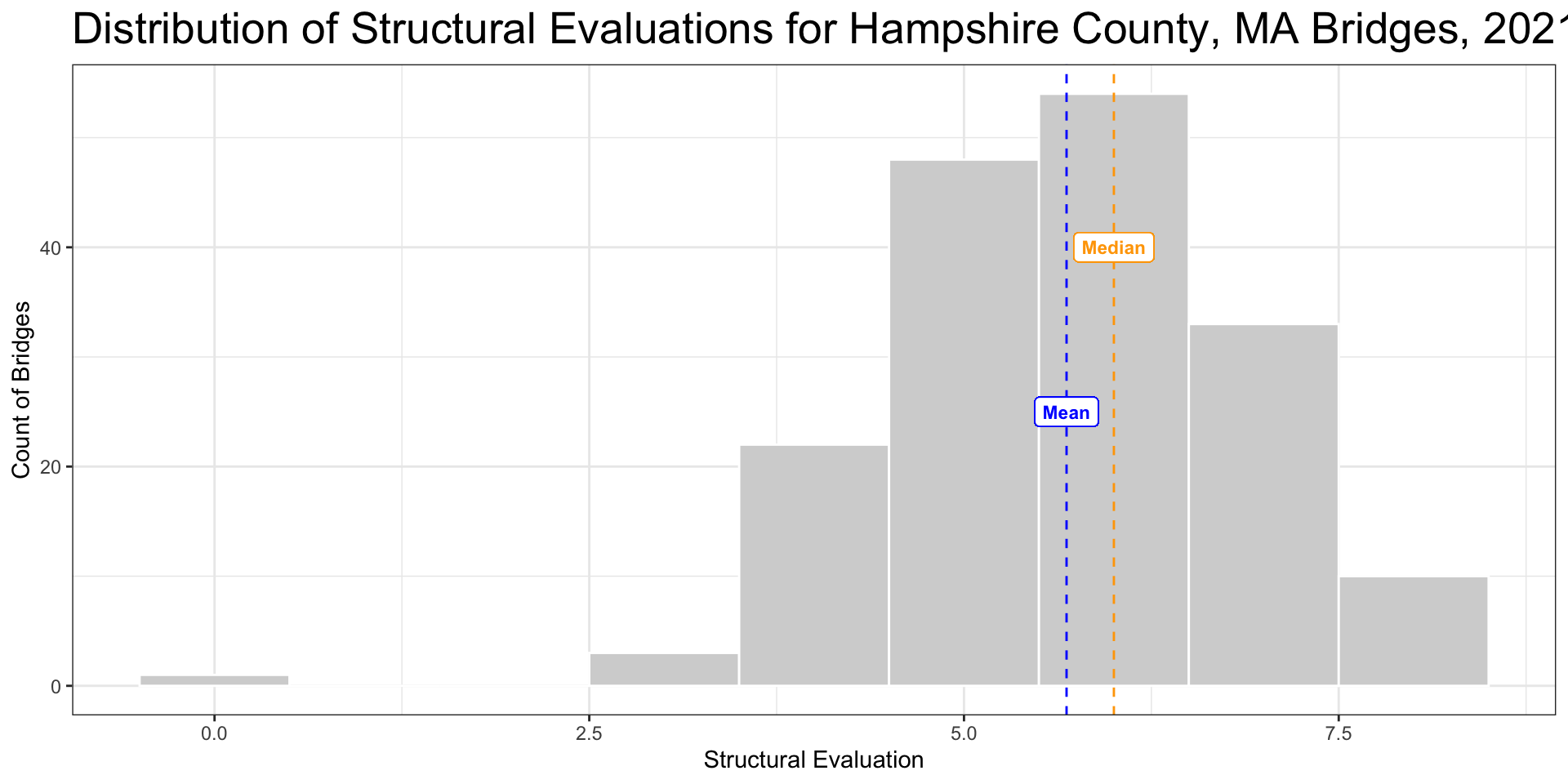
Learning Check: How many variables from the dataset are represented on the previous plot?

Normal Distributions

• More values huddle around some center line and taper off as we move away from center
• Histogram is symmetrical with a perfectly normal distribution
• Median and mean should be about the same; mean is a good measure of central tendency

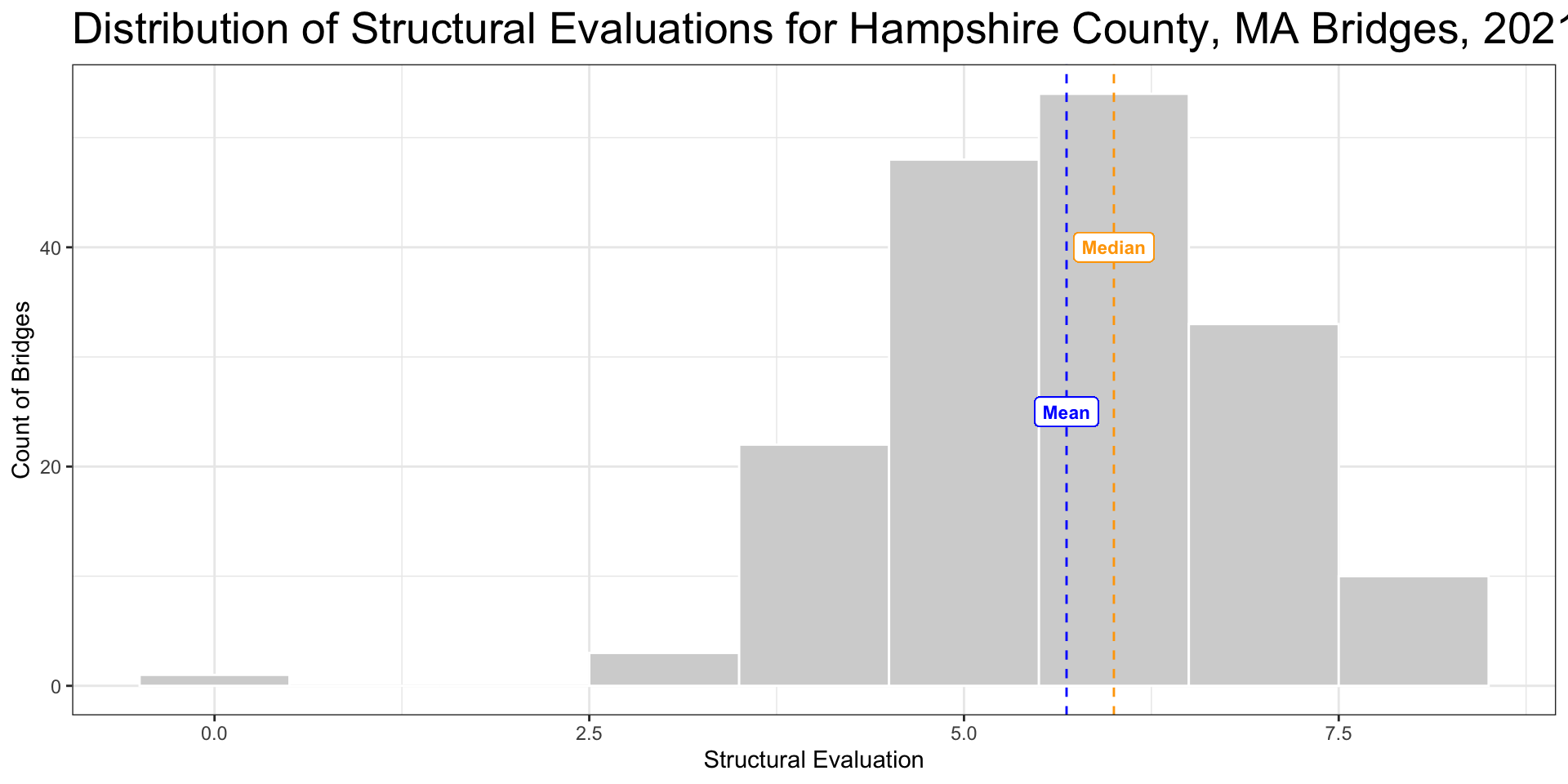
Skew

• Histogram is non-symmetrical when there is skew
• Long trail to the right of center indicates a right skew
• Median becomes more representative measure of central tendency than mean

Summarizing Data

• Measures of central tendency summarize swaths of information into single value
• Can be reductionist
  • Example: Measures of central tendency related to wealth in the US only tell us about those in the middle
  • Hide the experiences of the most impoverished communities.
• Degree of spread or dispersion is just as important as center

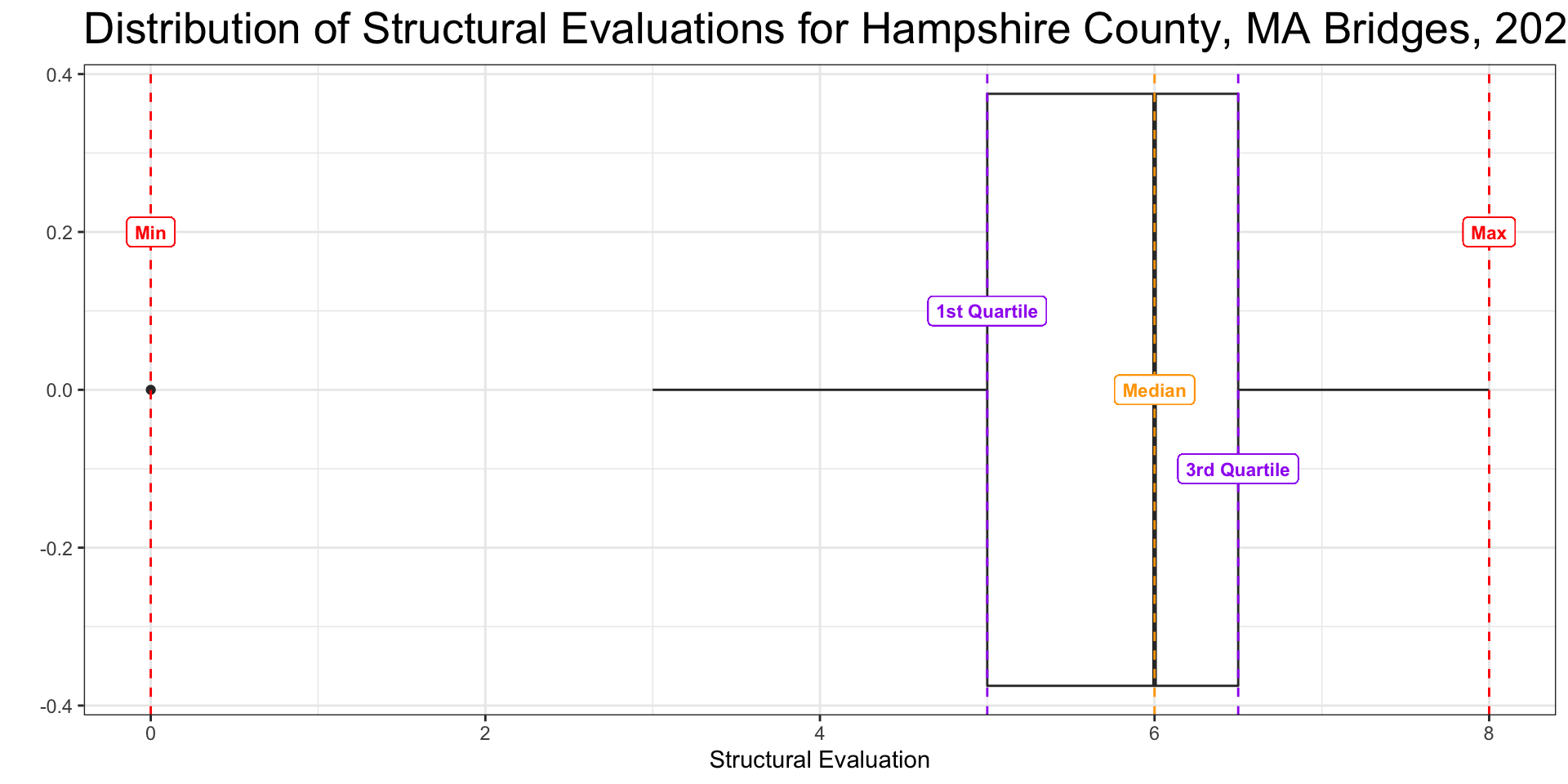
Range

• Maximum value minus the minimum value
• Evaluates the spread of the entire dataset

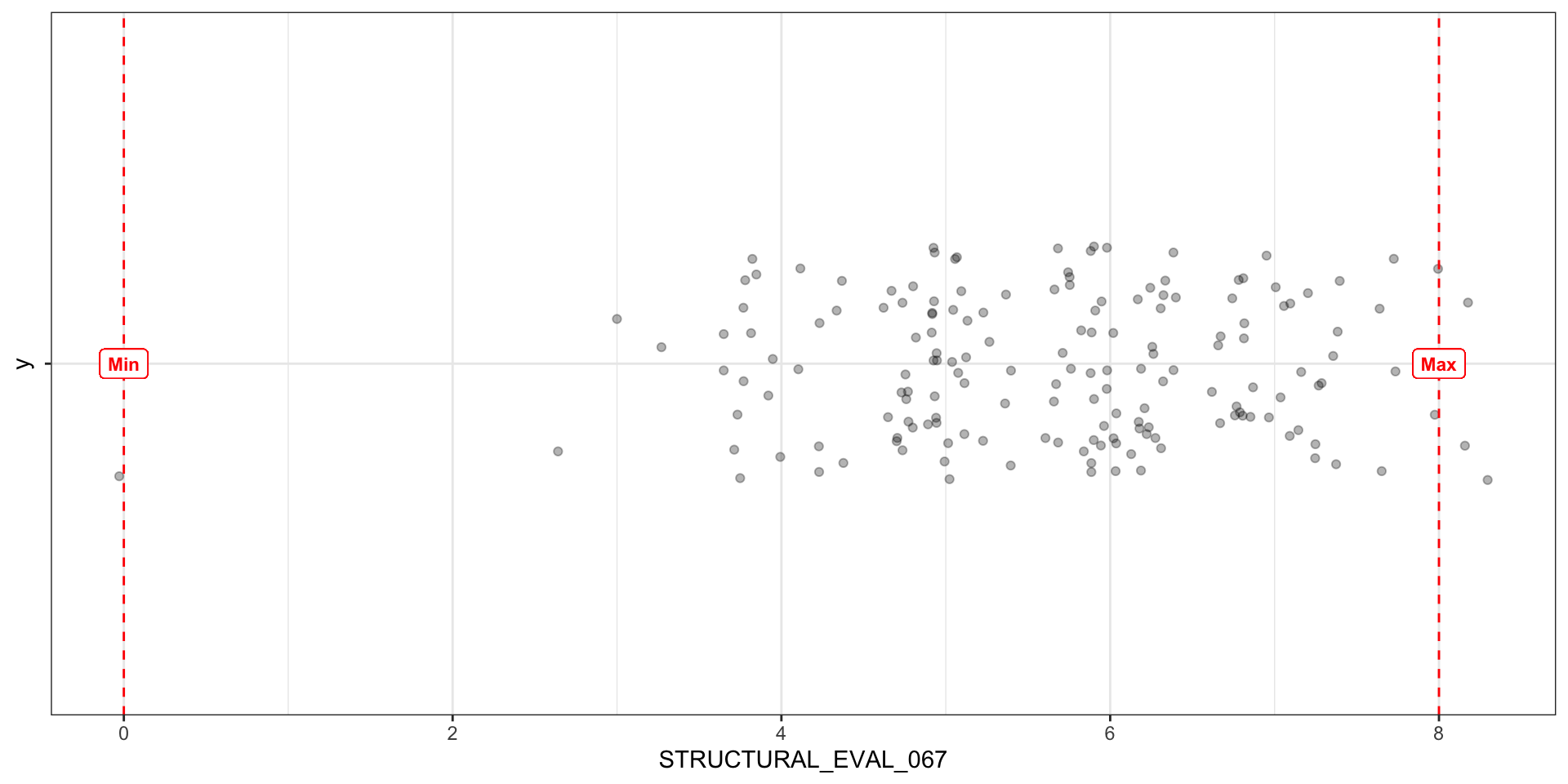
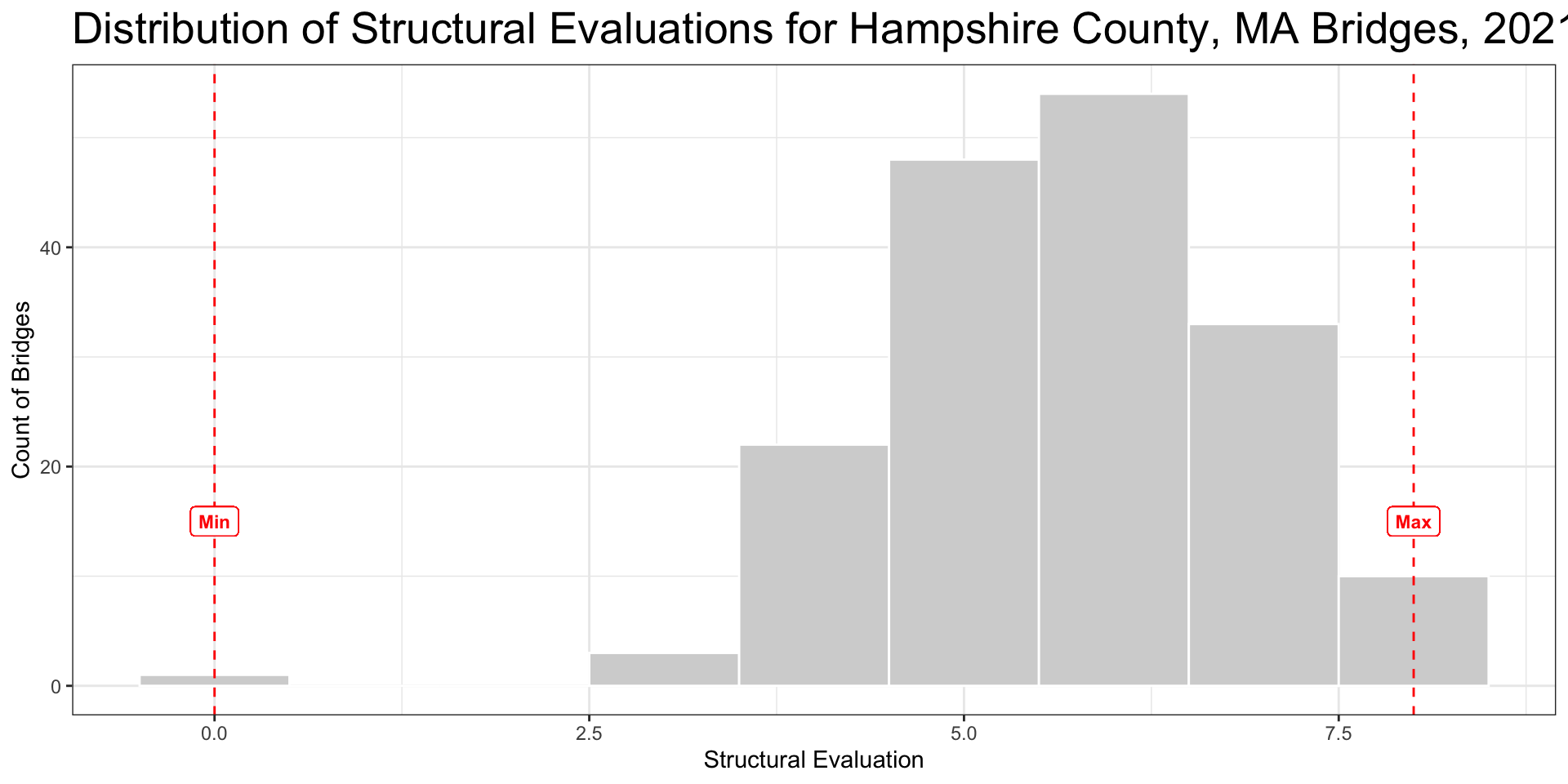
Interquartile Range

• 1st quartile is middle value between minimum and median
• 3rd quartile is middle value between median and maximum
• IQR is the difference between the 1st and 3rd quartile
• Represents the middle 50% of values

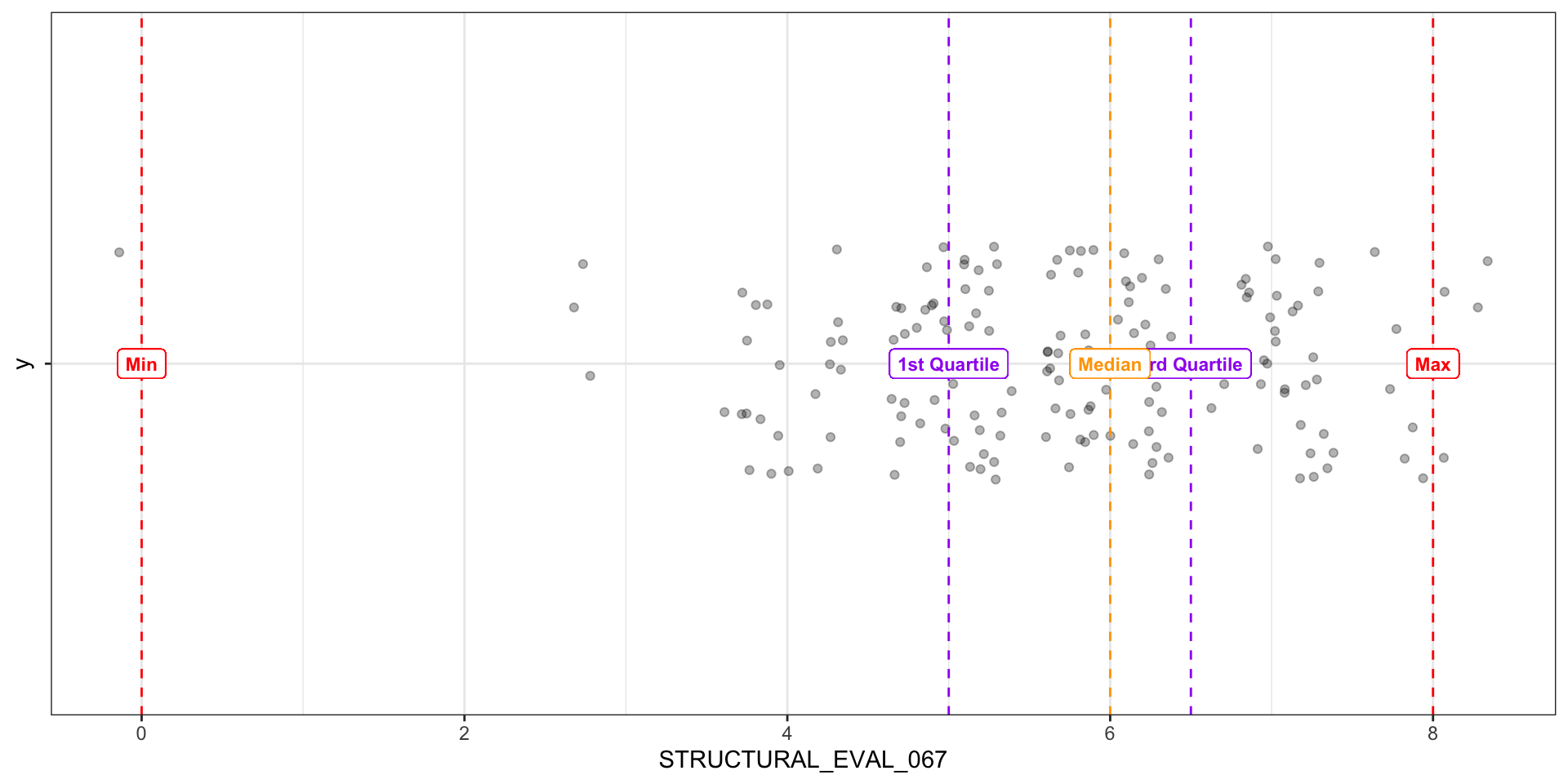
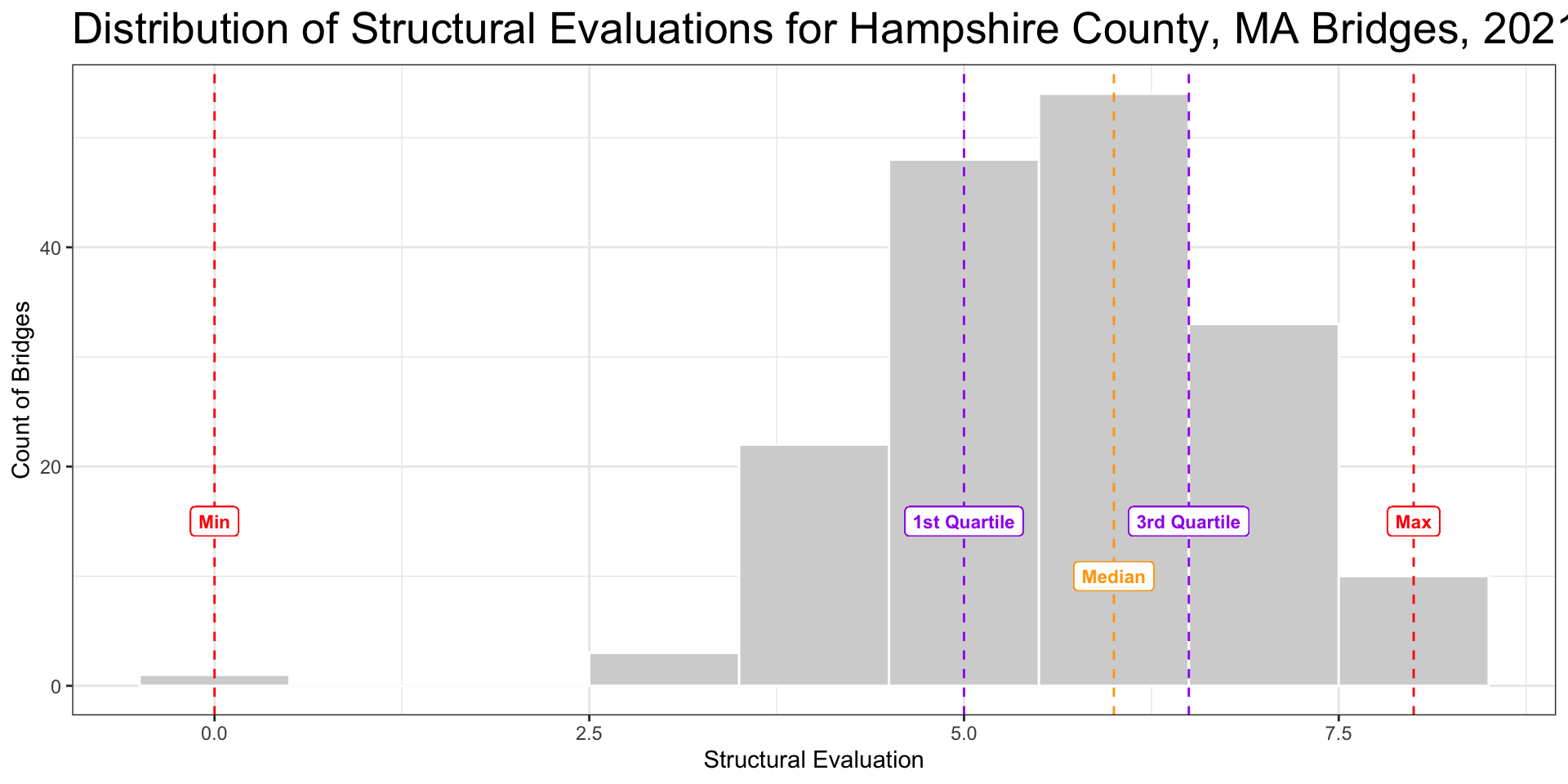
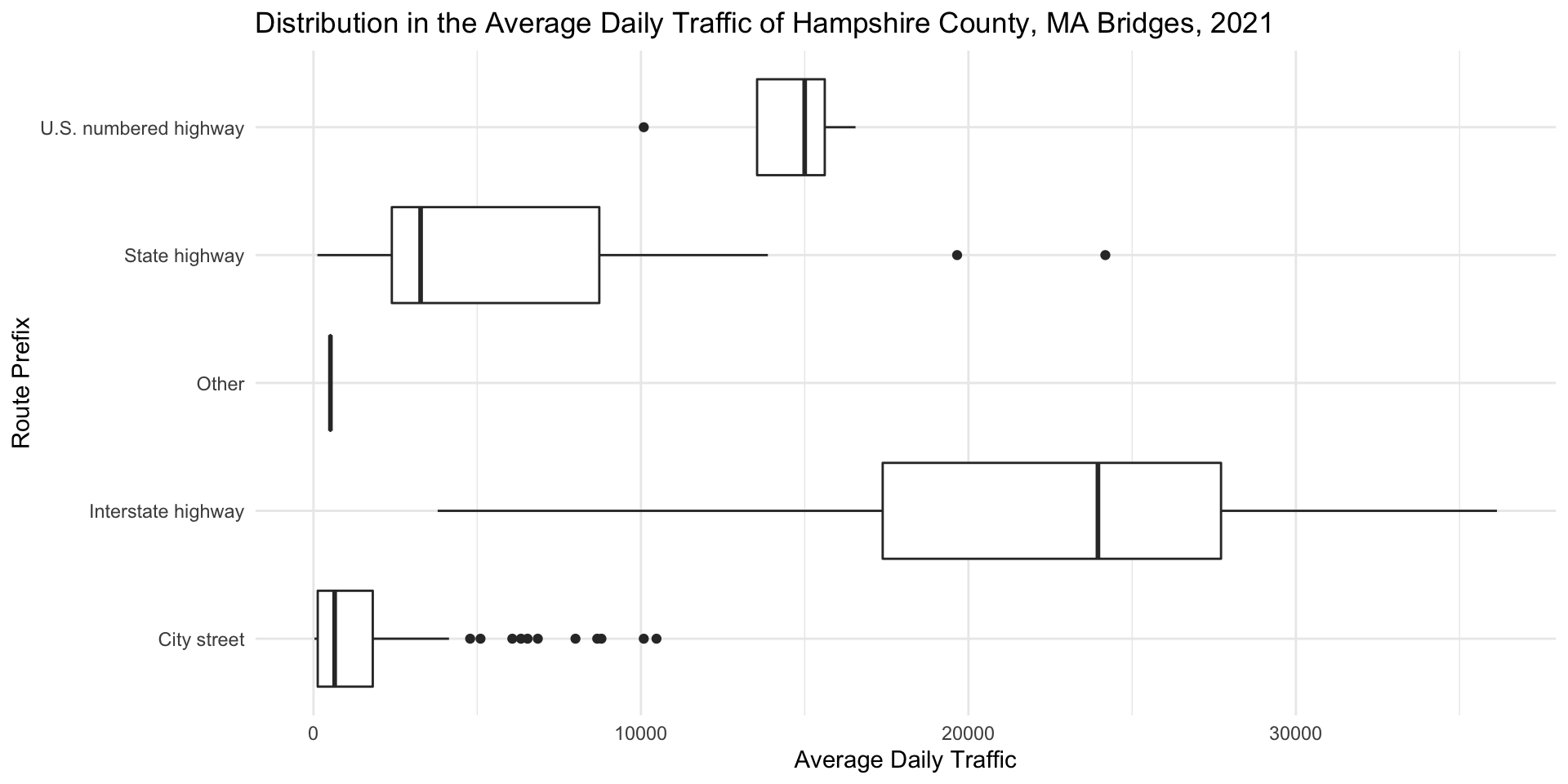
Boxplot

Grouped Boxplots

ggplot(nbi_hampshire, aes(x = ADT_029, y = ROUTE_PREFIX_005B_L)) +
  geom_boxplot() +
  labs(title = "Distribution in the Average Daily Traffic of Hampshire County, MA Bridges, 2021", 
       x = "Average Daily Traffic",
       y = "Route Prefix") +
  theme_minimal()

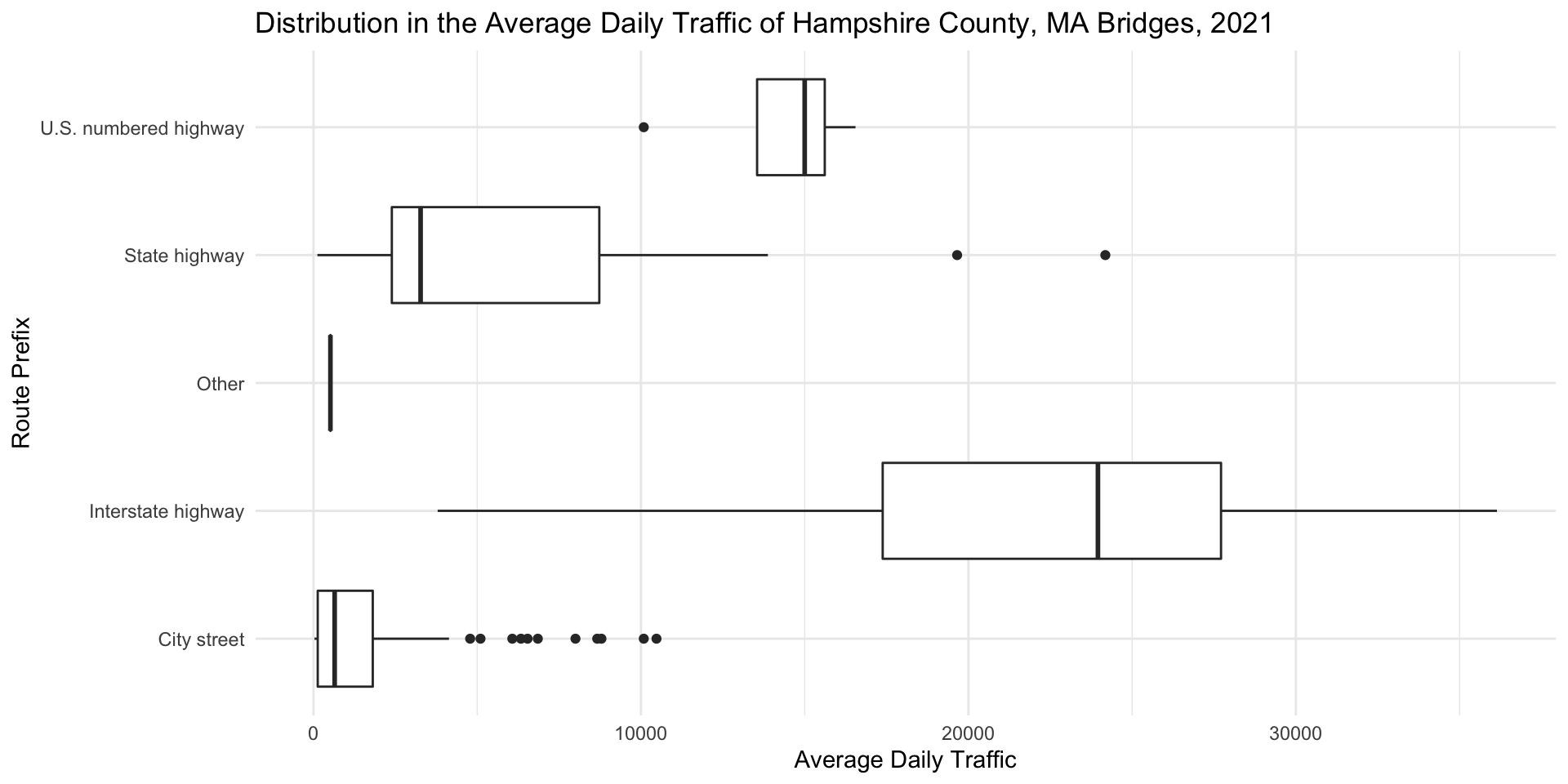
Interpreting Boxplots Step 1: Check for Outliers

How many are there? What do they indicate? Do you assume they are errors in teh data? Or do they represent extremes that are important for us to take into consideration?

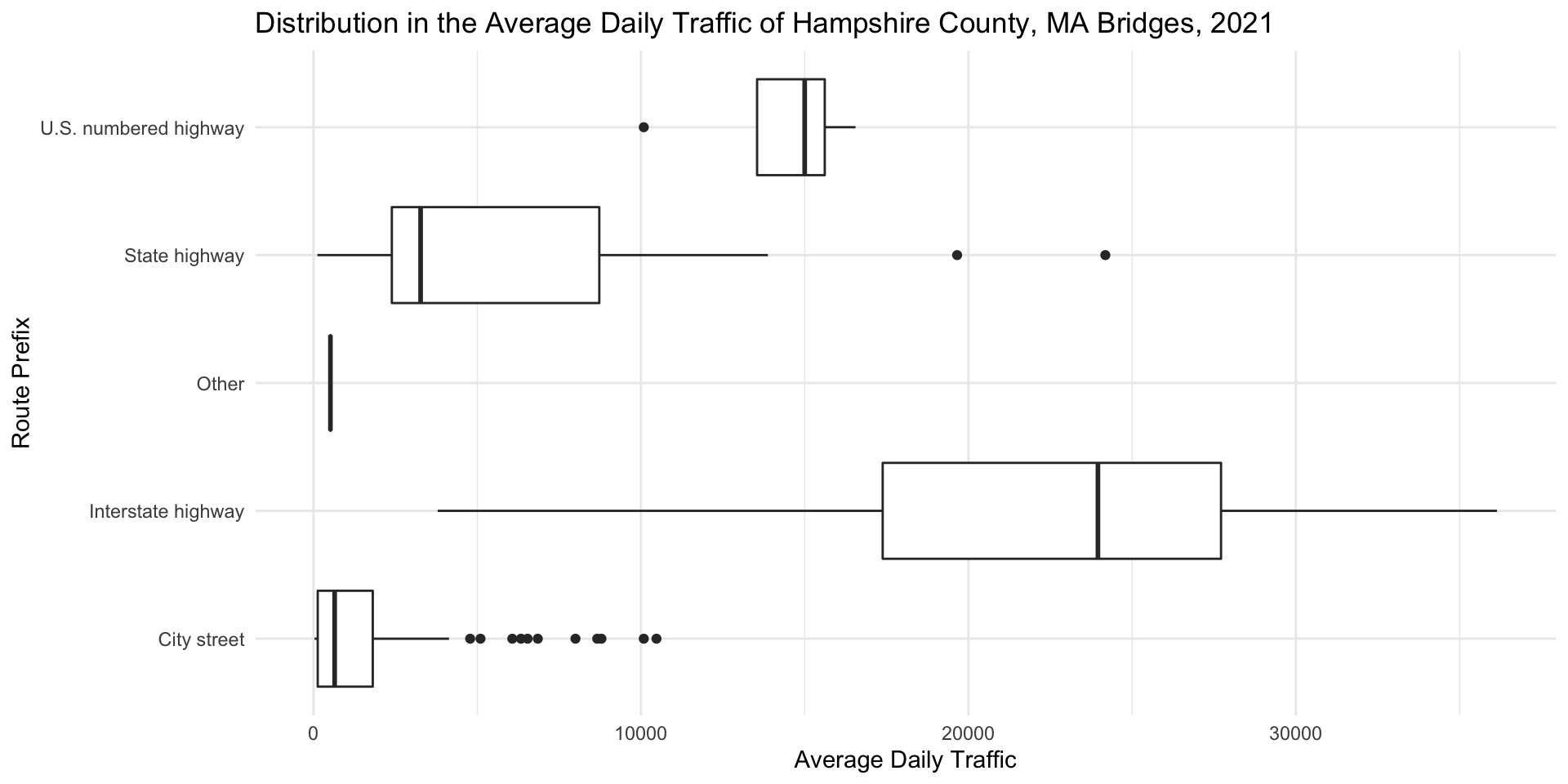
Interpreting Boxplots Step 2: Compare Medians

Do the medians line up? If not, in which groups are the medians higher and in which are they lower?

Interpreting Boxplots Step 3: Compare Range

Do certain groups have a wider range of values represented than others? In other words, are the values more distributed for certain groups than for others? This might indicate a greater degree of disparity in some groups than others.

Interpreting Boxplots Step 4: Compare IQR

In which groups do the middle 50% of values tend to huddle around a central value? In which are they more spread out from the center?

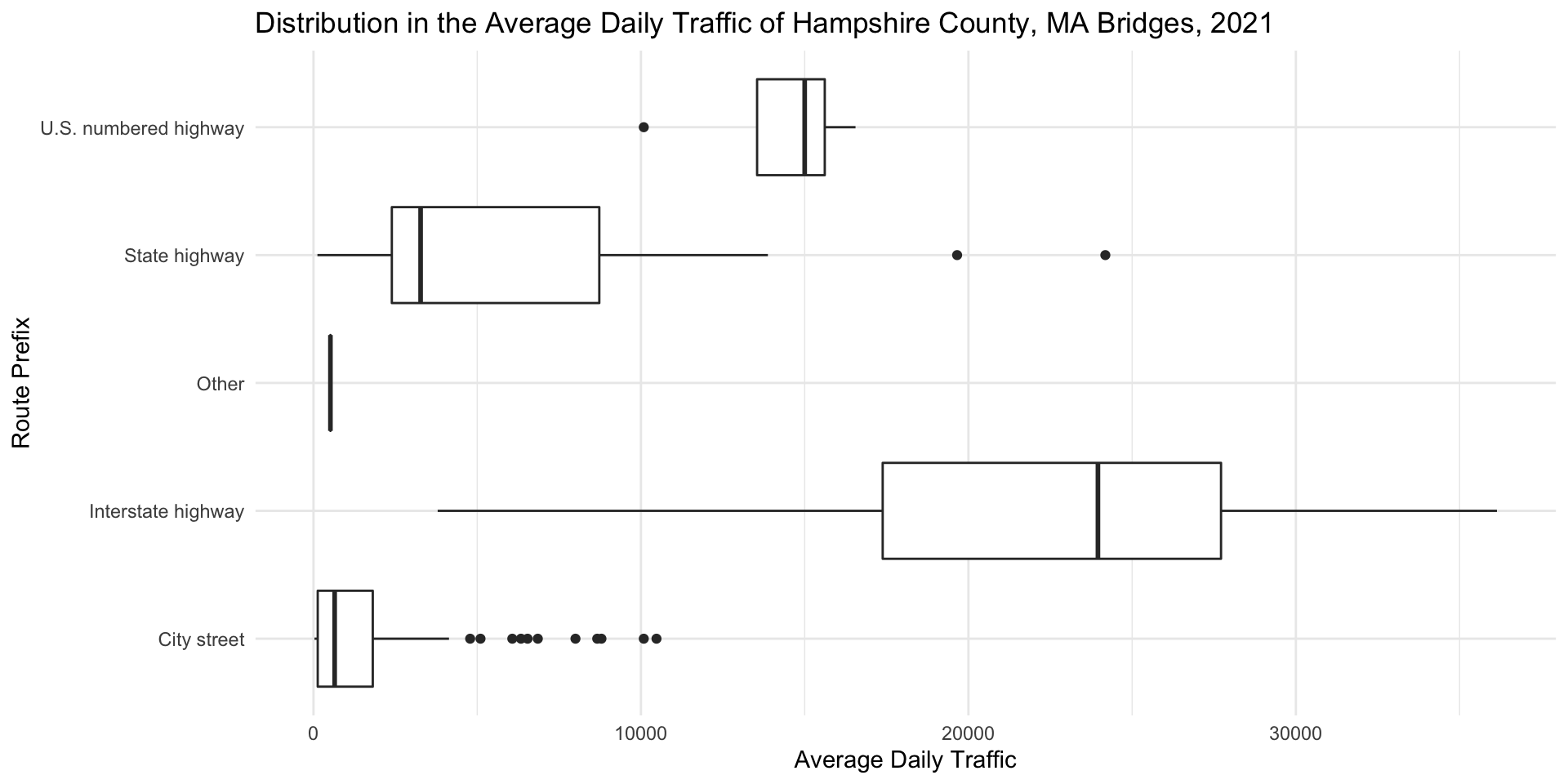
Interpreting Boxplots Step 5: Compare Symmetry

Does the median appear to be in the center of the range and IQR? Is the median closer to the minimum – or the bottom whisker? Or the top whisker?